suites variations Corrigé - 1re EDS

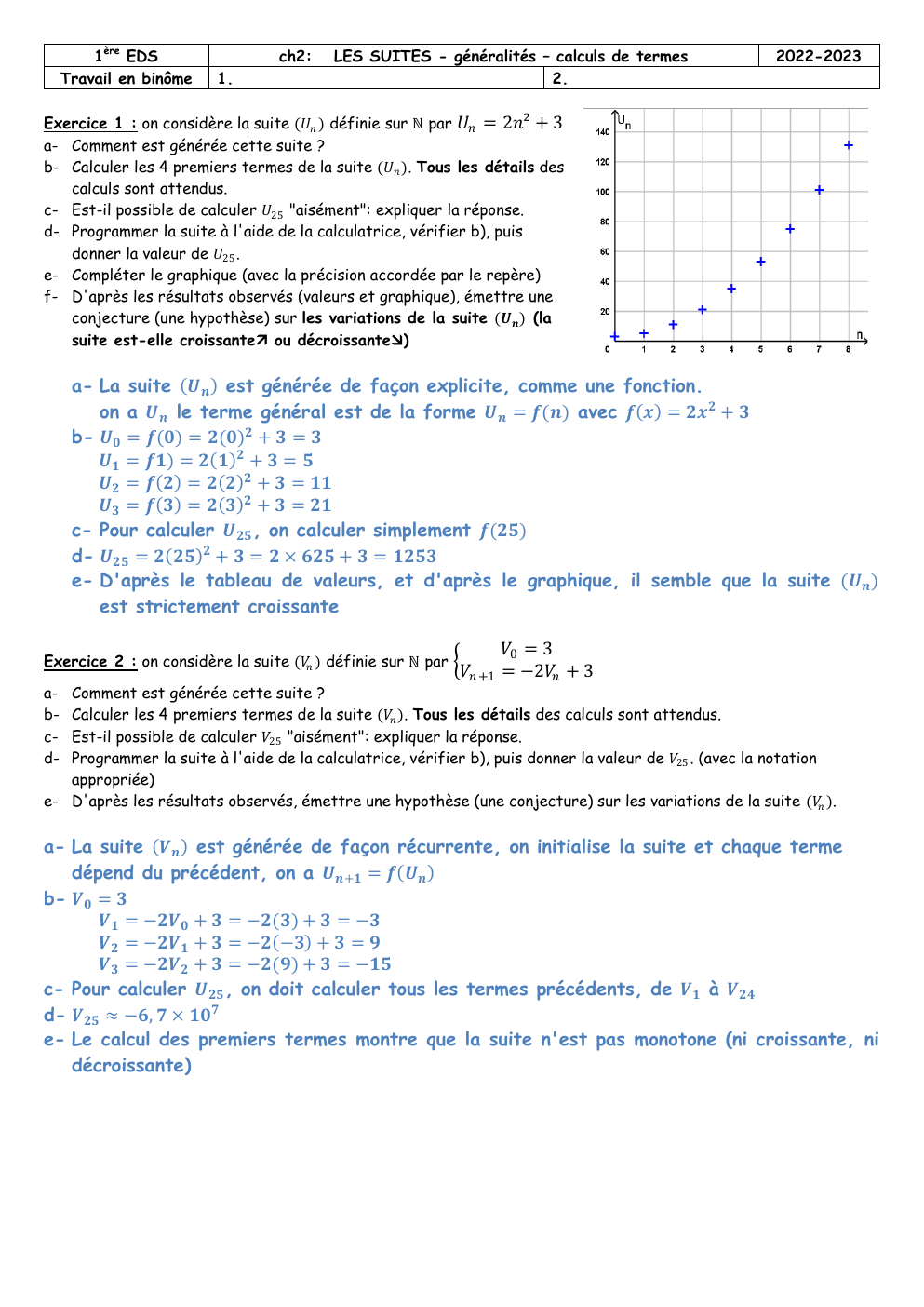
« 1ère EDS Travail en binôme ch2: 1. LES SUITES - généralités – calculs de termes 2. 2022-2023 Exercice 1 : on considère la suite (𝑈𝑛 ) définie sur ℕ par 𝑈𝑛 = 2𝑛² + 3 a- Comment est générée cette suite ? b- Calculer les 4 premiers termes de la suite (𝑈𝑛 ).

Tous les détails des calculs sont attendus. c- Est-il possible de calculer 𝑈25 "aisément": expliquer la réponse. d- Programmer la suite à l'aide de la calculatrice, vérifier b), puis donner la valeur de 𝑈25 . e- Compléter le graphique (avec la précision accordée par le repère) f- D'après les résultats observés (valeurs et graphique), émettre une conjecture (une hypothèse) sur les variations de la suite (𝑼𝒏 ) (la suite est-elle croissante ou décroissante) a- La suite 𝑼𝒏 est générée de façon explicite, comme une fonction. on a 𝑼𝒏 le terme général est de la forme 𝑼𝒏 = 𝒇(𝒏) avec 𝒇 𝒙 = 𝟐𝒙𝟐 + 𝟑 b- 𝑼𝟎 = 𝒇 𝟎 = 𝟐 𝟎 𝟐 + 𝟑 = 𝟑 𝑼𝟏 = 𝒇𝟏) = 𝟐 𝟏 𝟐 + 𝟑 = 𝟓 𝑼𝟐 = 𝒇 𝟐 = 𝟐 𝟐 𝟐 + 𝟑 = 𝟏𝟏 𝑼𝟑 = 𝒇 𝟑 = 𝟐 𝟑 𝟐 + 𝟑 = 𝟐𝟏 c- Pour calculer 𝑼𝟐𝟓 , on calculer simplement 𝒇(𝟐𝟓) d- 𝑼𝟐𝟓 = 𝟐 𝟐𝟓 𝟐 + 𝟑 = 𝟐 × 𝟔𝟐𝟓 + 𝟑 = 𝟏𝟐𝟓𝟑 e- D'après le tableau de valeurs, et d'après le graphique, il semble que la suite (𝑼𝒏 ) est strictement croissante Exercice 2 : on considère la suite (𝑉𝑛 ) définie sur ℕ par abcd- 𝑉𝑛+1 𝑉0 = 3 = −2𝑉𝑛 + 3 Comment est générée cette suite ? Calculer les 4 premiers termes de la suite (𝑉𝑛 ).

Tous les détails des calculs sont attendus. Est-il possible de calculer 𝑉25 "aisément": expliquer la réponse. Programmer la suite à l'aide de la calculatrice, vérifier b), puis donner la valeur de 𝑉25 .

(avec la notation appropriée) e- D'après les résultats observés, émettre une hypothèse (une conjecture) sur les variations de la suite (𝑉𝑛 ). a- La suite 𝑽𝒏 est générée de façon récurrente, on initialise la suite et chaque.... »