STATISTIQUES

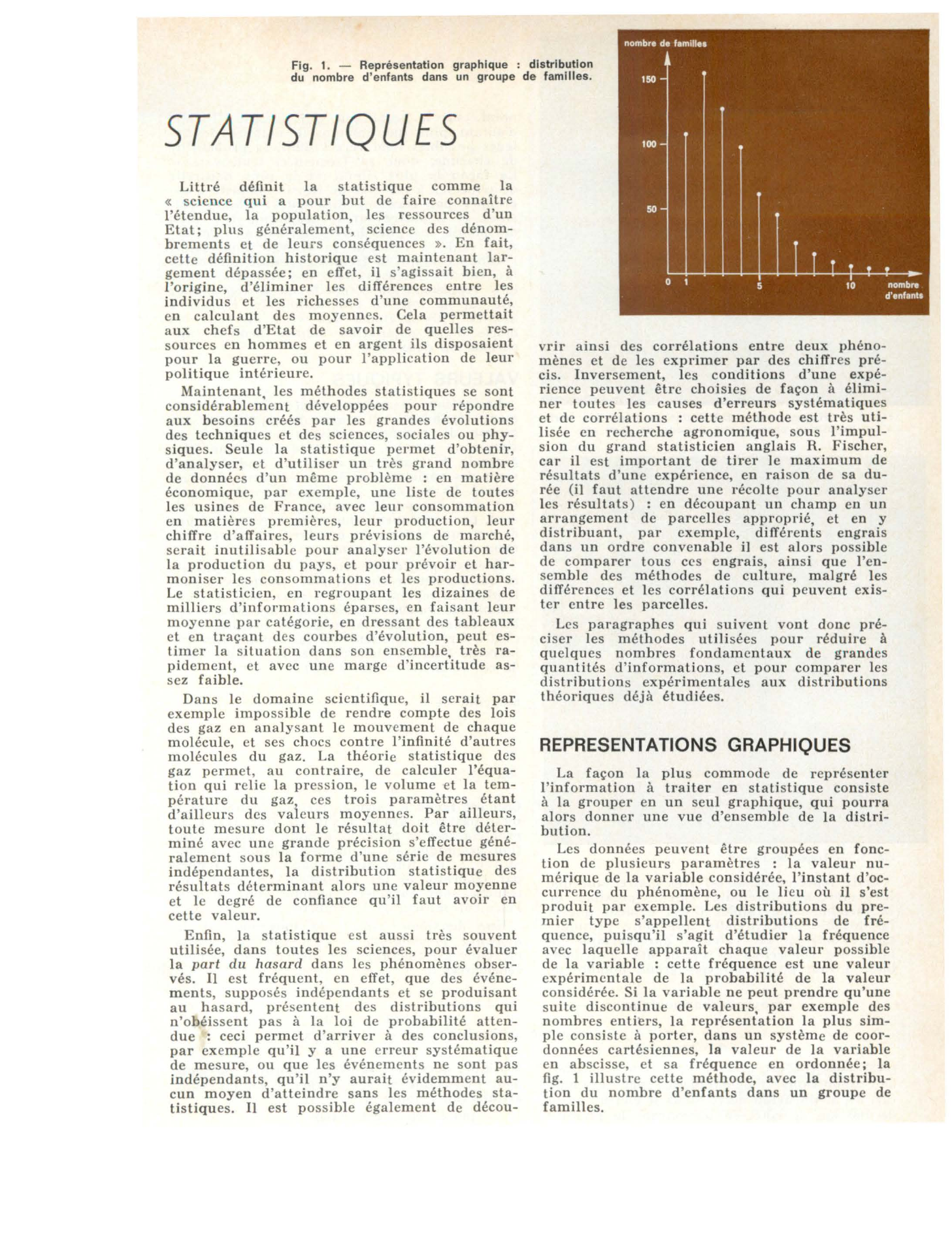
« Fig.

1.

-Représentation graphique : distri b ution du nombre d'enfants dans un groupe de fami lles.

STATISTIQ UE S Littré définit la statistique comme la « science qui a pour but de faire connaître l'étendue, la population, les ressources d'un Etat; plus généralement, science des dénom­ brements et de leurs conséquences ».

En fait, cette définition historique est maintenant lar­ gement dépassée; en effet, il s'agissait bien, à l'origine, d'éliminer les différences entre les individus et les richesses d'une communauté, en calculant des moyennes.

Cela permettait aux chefs d'Etat de savoir de quelles res­ sources en hommes et en argent ils disposaient pour la guerre, ou pour l'application de leur politique intérieure.

Maintenant, les méthodes statistiques se sont considérablement développées pour répondre aux besoins créés par les grandes évolutions des techniques et des sciences, sociales ou phy­ siques.

Seule la statistique permet d'obtenir, d'analyser, et d'utiliser un très grand nombre de données d'un même problème : en matière économique, par exemple, une liste de toutes les usines de France, avec leur consommation en matières premières, leur production, leur chiffre d'affaires, leurs prévisions de marché, se1·ait inutilisable pour analyser l'évolution de la production du pays, et pour prévoir cl har­ moniser les consommations et les productions.

Le statistic ien, en regroupant les dizaines de milliers d'informations éparses, en faisant leur moyenne par catégorie, en dressant des tableaux et en traçant des courbes d'évolution, peut es­ limer la situation dans son ensemble, très ra­ pidement, et avec une marge d'incertitude as­ sez faible.

Dans le domaine scientifique, il serait par exemple impossible de rendre compte des lois des gaz en analysant le mouvement de chaque molécule, et ses chocs contre l'infinité d'autres molécules du gaz.

La théorie statistique des gaz permet, au contraire, de calculer l'équa­ tion qui relie la pression, le volume el la tem­ pérature du gaz, ces trois paramètres étant d'ailleurs des valeurs moyennes.

Par ailleurs, toute mesure dont le résultat doit être déter­ miné avec un e grande précision s'effectue géné­ ralement sous la forme d'une série de mesures indépendantes, la distribution statistique des résultats déterminant alors une valeur moyenne et le degré de confiance qu'il faut avoir en cette valeur.

Enfin, la statistique est aussi très souvent utilisée, dans toutes les sciences, pour évaluer la part du hasard dans les phénomènes obser­ vés.

Il est fréquent , en effet, que des événe­ ments, supposés indépendants et se produisant au hasard, présentent des distributions qui n'obéissent pas à la loi de probabilité atten­ due : ceci permet d'ar river à des conclusions, par exemple qu'il y a une erreur systématique de mesure, ou que les événements ne sont pas indépendants, qu'il n'y aurait évidemment au­ cun moyen d'atteindre sans les méthodes sta­ tistiques.

Il est pos sible également de décou- vrir ainsi des corrélations entre deux phéno­ mènes et de les exprimer par des chiffres pré­ cis.

Inversement, les conditions d'une expé­ rience peuvent être choisies de façon à élimi­ ner toutes les causes d'erreurs systématiques et de corrélations : celte méthode est très uti­ lisée en recherche agronomique, sous l'impu l­ sion du grand statisticien anglais R.

Fischer, car il est important de tirer le maximum de résultats d'une expérience, en raison de sa du­ rée (il faut attendre une récolte pour analyser les résultats) : en découpant un champ en un arrangement de parcelles approprié, et en y distribuant, par exemple, différents engrais dans un ordre convenable il est alors possible de comparer tous ces engrais, ainsi que l'en­ semble des méthodes de culture, malgré les différences et les corrélations qui peuvent exis­ ter entre les parcelles.

Les paragraphes qui suivent vont donc pré­ ciser les méthodes utilisées pour réduire à quelques nombres fondam entaux de grandes quantités d'informations, et pour comparer les distributions expérimentales aux distributions théoriques déjà étudiées.

REPRESENTATIONS GRAPHIQUES La façon la plus commode de représenter l'information à traiter en statistique consiste à la grouper en un seul graphique, qui pourra alors donner une vue d'ensemble de la dis tri­ bution.

Les données peuvent être groupées en fonc­ tion de plusieurs paramètres : la valeur nu­ mérique de la variable considérée, l'instant d'oc­ currence du phénomène, ou le lieu où il s'est produit par exemple.

Les distributions du pre­ mier type s'appellent distributions de fré­ quence, puisqu'il s'agit d'étudier la fréquence avec laquelle apparaît chaque valeur possible de la variable : cette fréquence est une valeur expérimentale de la probabilité de la valeur considérée.

Si la variable ne peul prendre qu'une suite discontinue de valeurs, par exemple des nombres entiers, la représentation la plus sim­ ple consiste à porter, dans un système de coor­ données cartésiennes, la valeur de la variable en abscisse, et sa fréquence en ordonnée; la fig.

1 illustre cette méthode, avec la distribu­ tion du nombre d'enfants dans un groupe de familles.. »