Résumé dérivation première

« Rappels de 1ère Nombre dérivé Soit f une fonction définie sur un intervalle I et a un élément de I. f (a + h) − f (a) Si la limite lim existe, on la note « f ' ( a ) » et on l’appelle « nombre h → 0, h ≠ 0 h dérivé de la fonction f en a ».

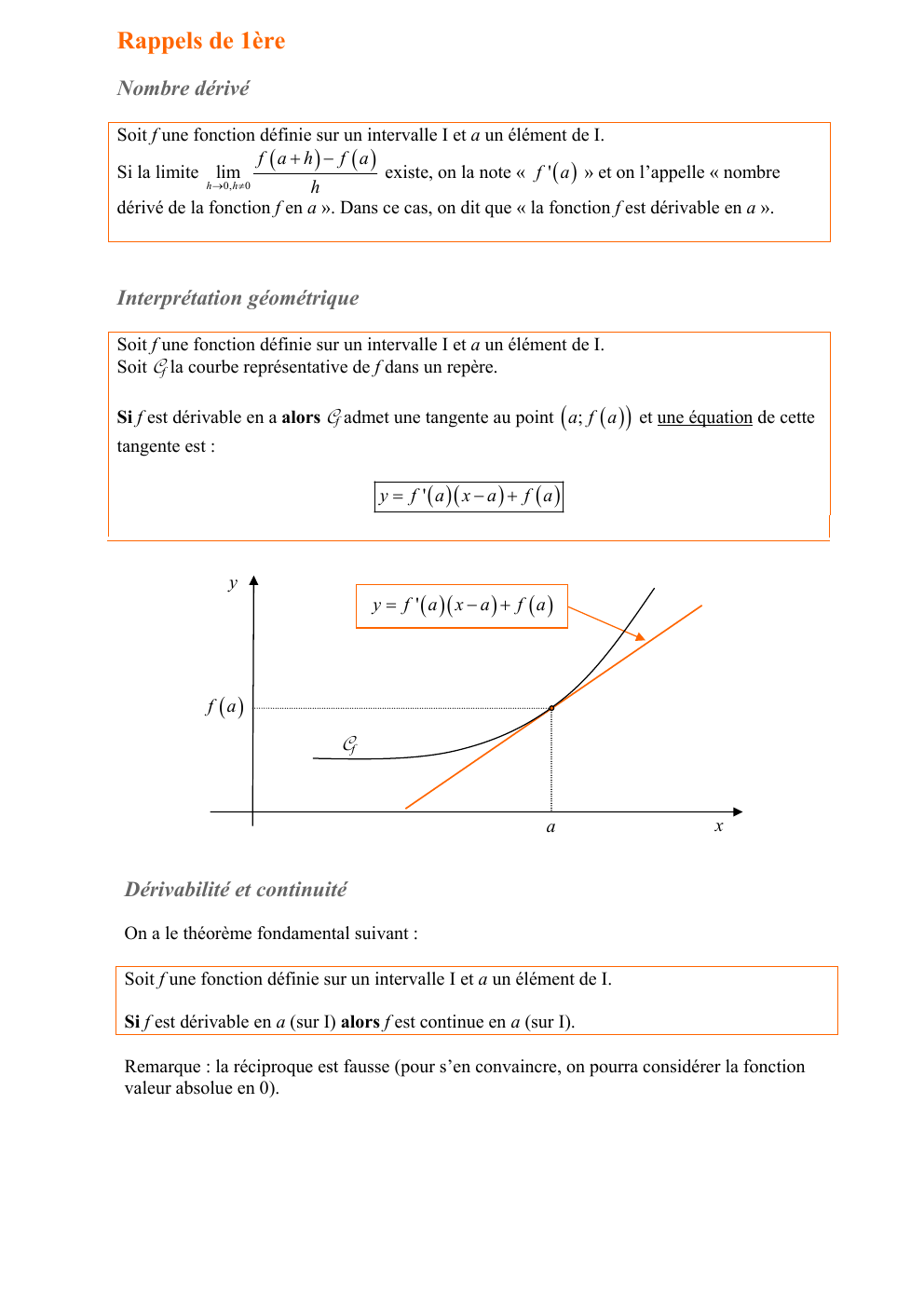
Dans ce cas, on dit que « la fonction f est dérivable en a ». Interprétation géométrique Soit f une fonction définie sur un intervalle I et a un élément de I. Soit Cf la courbe représentative de f dans un repère. Si f est dérivable en a alors Cf admet une tangente au point ( a; f ( a ) ) et une équation de cette tangente est : y = f ' ( a )( x − a ) + f ( a ) y y = f ' ( a )( x − a ) + f ( a ) f (a) Cf a x Dérivabilité et continuité On a le théorème fondamental suivant : Soit f une fonction définie sur un intervalle I et a un élément de I. Si f est dérivable en a (sur I) alors f est continue en a (sur I). Remarque : la réciproque est fausse (pour s’en convaincre, on pourra considérer la fonction valeur absolue en 0).. »