pour des maths

« SUITES NUMÉRIQUES P.G.

2008/2009 1 §1.

Pour bien débuter 1.

Rappels de première On distingue traditionnellement deux types principaux de suites : Suite définie par son terme général : Le terme général u n de la suite est donné directement en fonction de n, ce qui permet de calculer directement n’importe quel terme de la suite et, en général, d’utiliser les propriétés de la fonction associée à la suite.

Exemple : La suite u définie sur N par 21 n n u n = + a pour fonction associée la fonction : 21 x fx x+ !.

8 88 (8) 281 17 uf== = ×+.

Les variations de la fonction donnent directe- ment celles de la suite et la limite en + ∞ de la fonction donne la limite de la suite.

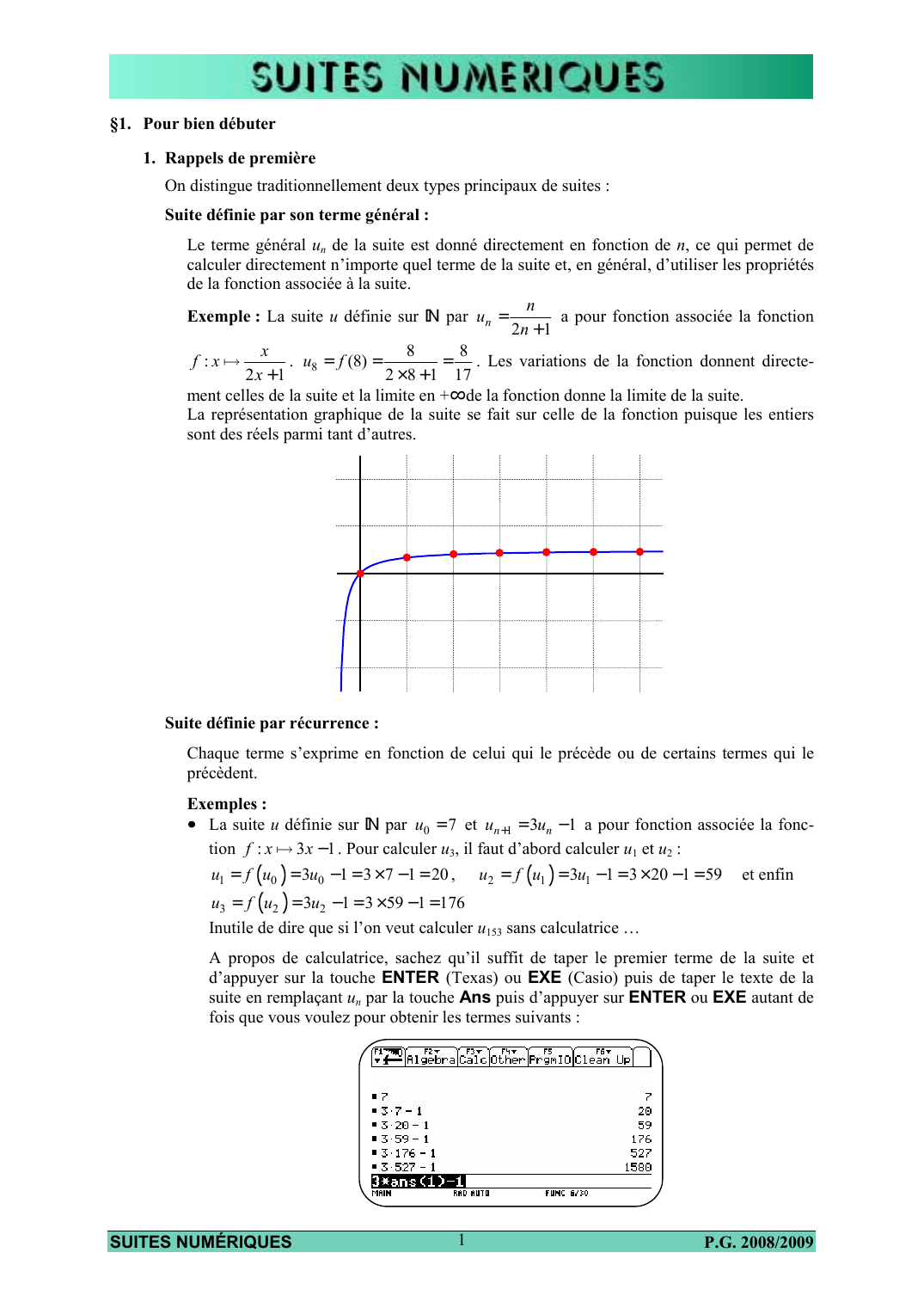
La représentation graphique de la suite se fait sur celle de la fonction puisque les entiers sont des réels parmi tant d’autres.

Suite définie par récurrence : Chaque terme s’exprime en fonction de celui qui le précède ou de certains termes qui le précèdent.

Exemples : • •• • La suite u définie sur N par 0 7 u= et 1 31 nnuu+ =− a pour fonction associée la fonc- tion :31 fx x− ! .

Pour calculer u3, il faut d’abord calculer u 1 et u 2 : () 100 3137120 ufu u==−=×−=, () 211 31320159 ufu u==−=×−= et enfin () 322 313591176 ufu u==−=×−= Inutile de dire que si l’on veut calculer u 153 sans calculatrice … A propos de calculatrice, sachez qu’il suffit de taper le premier terme de la suite et d’appuyer sur la touche ENTER (Texas) ou EXE (Casio) puis de taper le texte de la suite en remplaçant u n par la touche Ans puis d’appuyer sur ENTER ou EXE autant de fois que vous voulez pour obtenir les termes suivants :. »