Maths: CHAPITRE 4 : Limites de suites

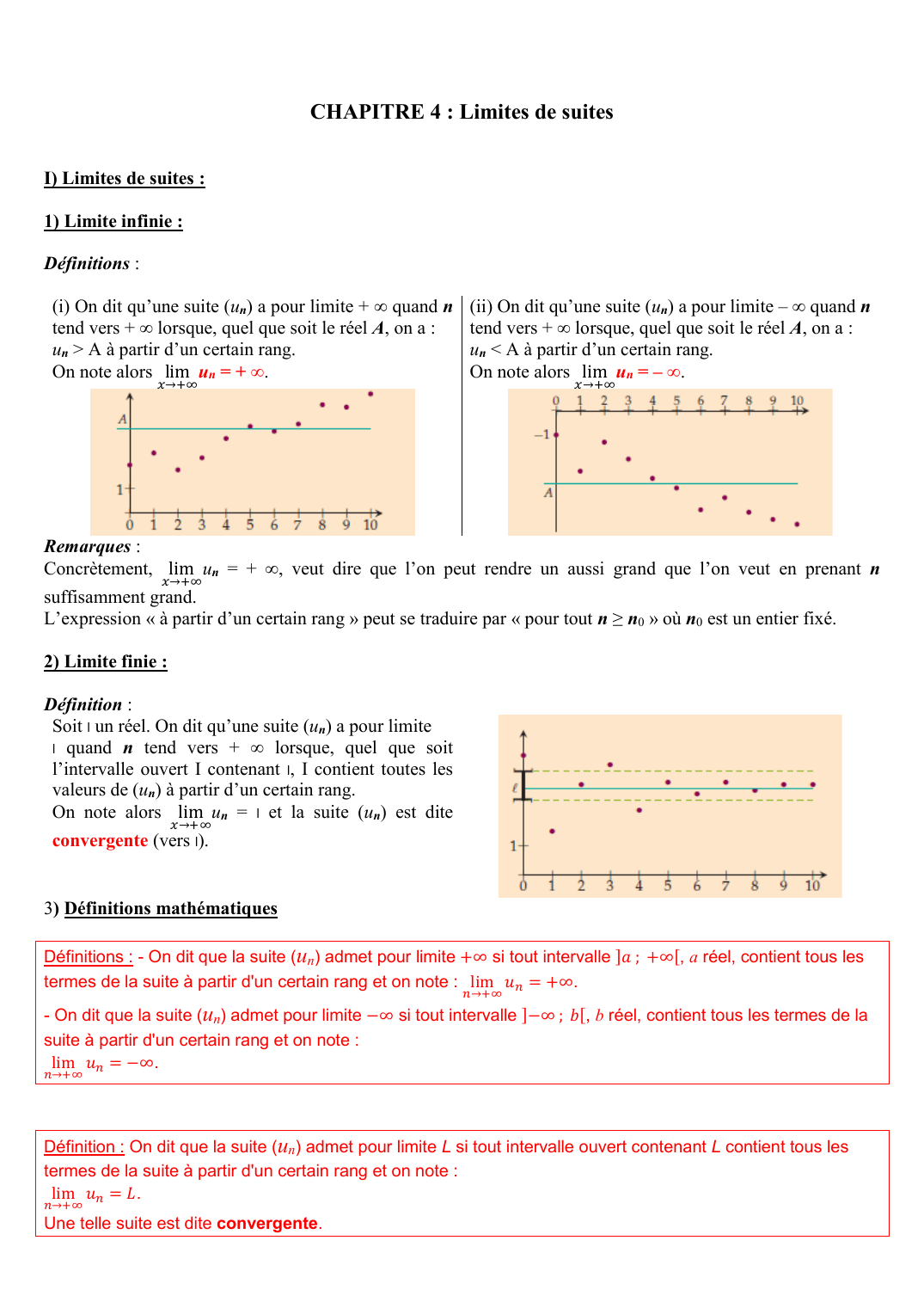
« CHAPITRE 4 : Limites de suites I) Limites de suites : 1) Limite infinie : Définitions : (i) On dit qu’une suite ( un) a pour limite + ∞ quand n tend vers + ∞ lorsque, quel que soit le réel A, on a : un > A à partir d’un certain rang. On note alors lim��→+∞un = + ∞ .

(ii) On dit qu’une suite ( un) a pour limite – ∞ quand n tend vers + ∞ lorsque, quel que soit le réel A, on a : un < A à partir d’un certain rang. On note alors lim��→+∞un = – ∞.

Remarques : Concrètement, lim��→+∞un = + ∞, veut dire que l’on peut rendre un aussi grand que l’on veut en prenant n suffisamment grand. L’expression « à partir d’un certain rang » peut se traduire par « pour tout n ≥ n0 » où n0 est un entier fixé. 2) Limite finie : Définition : Soit l un réel. On dit qu’une suite ( un) a pour limite l quand n tend vers + ∞ lorsque, quel que soit l’intervalle ouvert I contenant l, I contient toutes les valeurs de ( un) à partir d’un certain rang. On note alors lim��→+∞un = l et la suite ( un) est dite convergente (vers l).

3) Définitions mathématiques Définitions : - On dit que la suite ( un) admet pour limite +∞ si tout intervalle ]� ; +∞[, a réel, contient tous les termes de la suite à partir d'un certain rang et on note : lim��→+∞���= +∞.

- On dit que la suite ( un) admet pour limite −∞ si tout intervalle ]−∞ ; �[, b réel, contient tous les termes de la suite à partir d'un certain rang et on note : lim��→+∞���= −∞.

Définition : On dit que la suite ( un) admet pour limite L si tout intervalle ouvert contenant L contient tous les termes de la s uite à partir d'un certain rang et on note : lim��→+∞���= ��.

Une telle suite est dite convergente .. »