Maths Chap V : Dérivation en un point

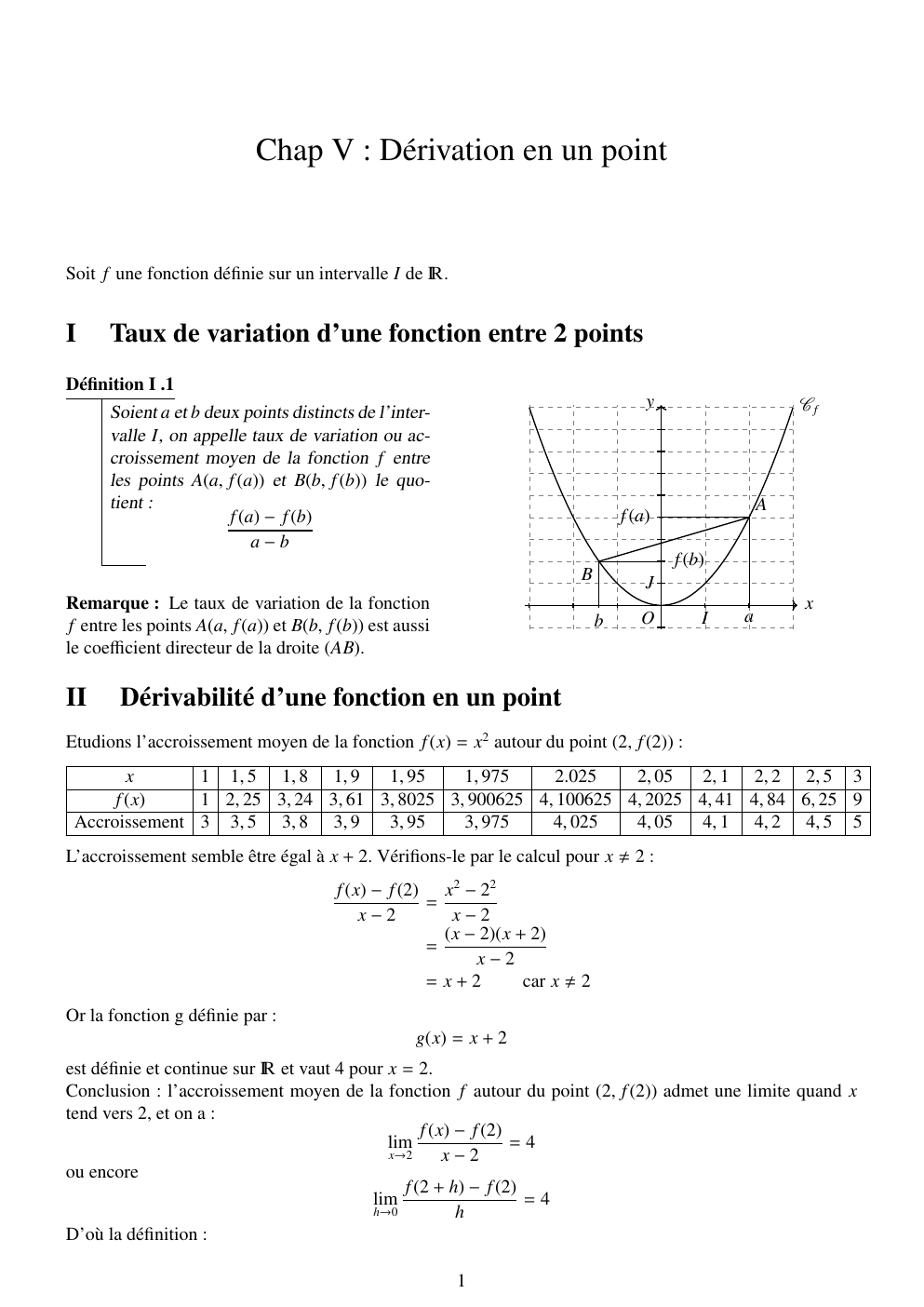
« Chap V : Dérivation en un point Soit f une fonction définie sur un intervalle I de IR. I Taux de variation d’une fonction entre 2 points Définition I .1 A f (a) f (b) B Remarque : Le taux de variation de la fonction f entre les points A(a, f (a)) et B(b, f (b)) est aussi le coefficient directeur de la droite (AB). II Cf y Soient a et b deux points distincts de l’intervalle I, on appelle taux de variation ou accroissement moyen de la fonction f entre les points A(a, f (a)) et B(b, f (b)) le quotient : f (a) − f (b) a−b J b O I a x Dérivabilité d’une fonction en un point Etudions l’accroissement moyen de la fonction f (x) = x2 autour du point (2, f (2)) : x 1 1, 5 1, 8 1, 9 1, 95 1, 975 2.025 2, 05 2, 1 2, 2 2, 5 3 f (x) 1 2, 25 3, 24 3, 61 3, 8025 3, 900625 4, 100625 4, 2025 4, 41 4, 84 6, 25 9 Accroissement 3 3, 5 3, 8 3, 9 3, 95 3, 975 4, 025 4, 05 4, 1 4, 2 4, 5 5 L’accroissement semble être égal à x + 2.

Vérifions-le par le calcul pour x , 2 : f (x) − f (2) x2 − 22 = x−2.... »