limites et continuité cours + exercices

« 1 Limites et continuité A) Limites de fonctions. 1.

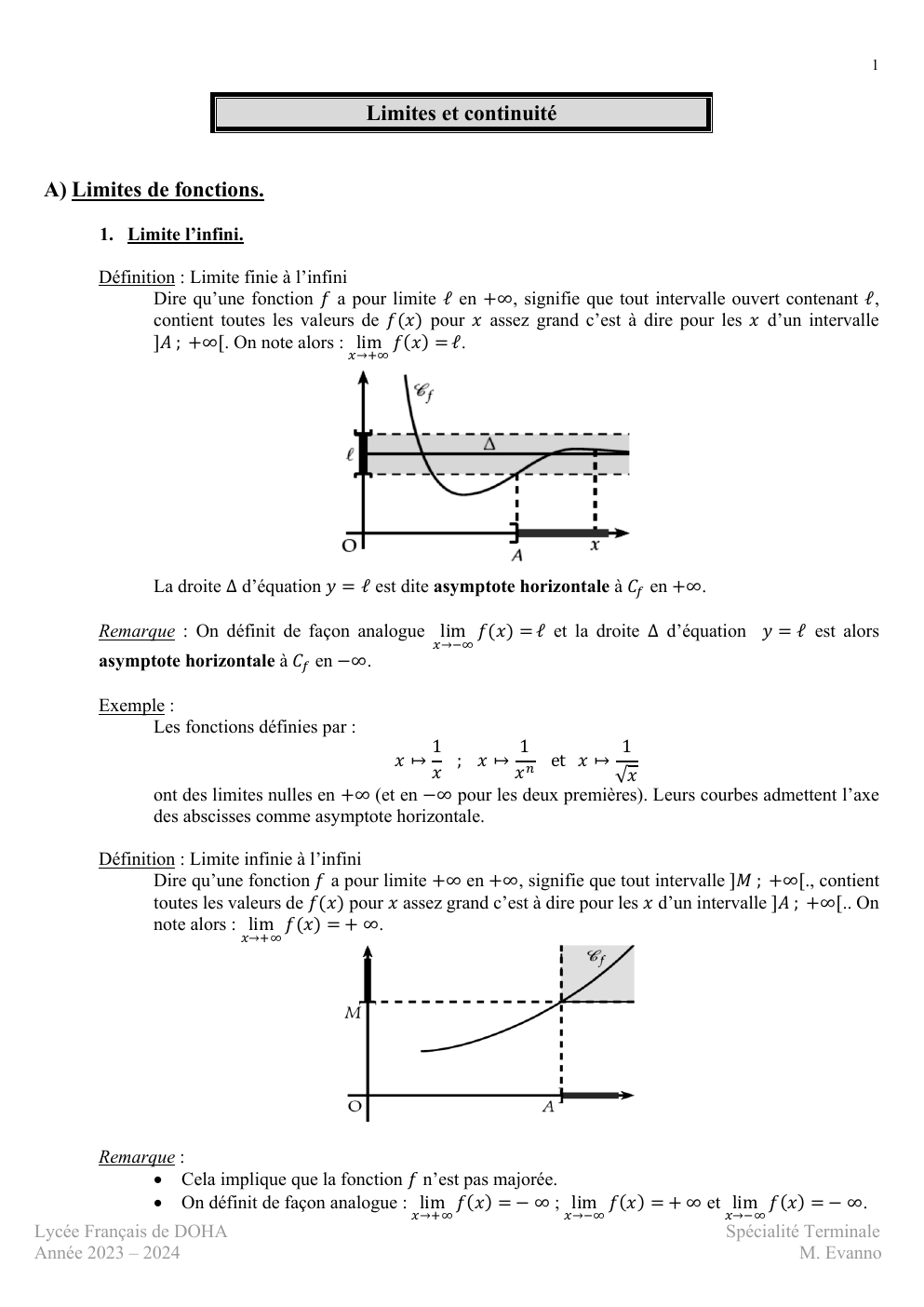
Limite l’infini. Définition : Limite finie à l’infini Dire qu’une fonction 𝑓 a pour limite ℓ en +∞, signifie que tout intervalle ouvert contenant ℓ, contient toutes les valeurs de 𝑓(𝑥) pour 𝑥 assez grand c’est à dire pour les 𝑥 d’un intervalle ]𝐴 ; +∞[.

On note alors : lim 𝑓(𝑥) = ℓ. 𝑥→+∞ La droite ∆ d’équation 𝑦 = ℓ est dite asymptote horizontale à 𝐶𝑓 en +∞. Remarque : On définit de façon analogue lim 𝑓(𝑥) = ℓ et la droite ∆ d’équation 𝑦 = ℓ est alors 𝑥→−∞ asymptote horizontale à 𝐶𝑓 en −∞. Exemple : Les fonctions définies par : 1 1 1 ; 𝑥 ↦ 𝑛 et 𝑥 ↦ 𝑥 𝑥 √𝑥 ont des limites nulles en +∞ (et en −∞ pour les deux premières).

Leurs courbes admettent l’axe des abscisses comme asymptote horizontale. 𝑥↦ Définition : Limite infinie à l’infini Dire qu’une fonction 𝑓 a pour limite +∞ en +∞, signifie que tout intervalle ]𝑀 ; +∞[., contient toutes les valeurs de 𝑓(𝑥) pour 𝑥 assez grand c’est à dire pour les 𝑥 d’un intervalle ]𝐴 ; +∞[..

On note alors : lim 𝑓(𝑥) = + ∞. 𝑥→+∞ Remarque : • Cela implique que la fonction 𝑓 n’est pas majorée. • On définit de façon analogue : lim 𝑓(𝑥) = − ∞ ; lim 𝑓(𝑥) = + ∞ et lim 𝑓(𝑥) = − ∞. 𝑥→+∞ Lycée Français de DOHA Année 2023 – 2024 𝑥→−∞ 𝑥→−∞ Spécialité Terminale M.

Evanno 2 2.

Limite infinie en un point. Définition : Dire qu’une fonction 𝑓 a pour limite +∞ en 𝑎, signifie que tout intervalle ]𝑀 ; +∞[ contient toutes les valeurs de 𝑓(𝑥) pour 𝑥 assez proche de 𝑎 c’est à dire pour les 𝑥 d’un intervalle ouvert contenant 𝑎.

On note alors : lim 𝑓(𝑥) = + ∞. 𝑥→𝑎 La droite ∆ d’équation 𝑥 = 𝑎 est dite asymptote verticale à 𝐶𝑓 . Vidéo : déterminer graphiquement des limites d'une fonction Remarque : • On définit de façon analogue lim 𝑓(𝑥) = − ∞. • 𝑥→𝑎 On peut aussi définir la limite à gauche ou à droite de 𝑥 = 𝑎 lorsque la limite en 𝑥 = 𝑎 n’existe pas.

On notera alors : ➢ limite à gauche : lim− 𝑓(𝑥) ou 𝑥→𝑎 lim 𝑓(𝑥). 𝑥→𝑎 𝑥𝑎 Exemples : • • 1 a pour limite 0 en + ∞ 𝑥2 1 La fonction 𝑥 ↦ n′ admet pas de limite en 0 𝑥 Elle admet en revanche une limite à gauche (−∞) et à droite (−∞)de 0 La fonction 𝑥 ↦ Lycée Français de DOHA Année 2023 – 2024 Spécialité Terminale M.

Evanno 3 3.

Limites des fonctions élémentaires. Propriété : limites en l’infini 1 𝑓(𝑥) 𝑥𝑛 1 𝑥𝑛 √𝑥 lim 𝑓(𝑥) +∞ 0 +∞ lim 𝑓(𝑥) +∞ si 𝑛 pair −∞ si 𝑛 impair 0 non défini 𝑥→+∞ 𝑥→−∞ 𝑒𝑥 1 𝑒𝑥 0 +∞ 0 non défini 0 +∞ √𝑥 Propriétés : limites en zéro 1 𝑓(𝑥) 1 𝑥𝑛 √𝑥 lim 𝑓(𝑥) +∞ +∞ lim 𝑓(𝑥) +∞ si 𝑛 pair −∞ si 𝑛 impair non défini 𝑥→0 𝑥>0 𝑥→0 𝑥 5 Les fonctions affines 𝑥 ⟼ −𝑥 + 2, 𝑥 ⟼ 𝑥 − 4 et 𝑥 ⟼ −2𝑥 + 13 sont continues sur ℝ. • Continuité en 3 ? lim− 𝑓(𝑥) = lim− − 𝑥 + 2 = −3 + 2 = −1 et 𝑥→3 𝑥→3 𝑓(3) = 3 − 4 = −1 Donc 𝑓 est continue en 3 et donc sur ] − ∞ ; 5[. • Continuité en 5 ? lim+ 𝑓(𝑥) = lim+ − 2𝑥 + 13 = −10 + 13 = 3 et 𝑥→5 𝑥→5 𝑓(5) = 5 − 4 = 1 Donc 𝑓 n’est pas continue en 5. • Donc 𝑓 est continue en 3 et donc sur ] − ∞ ; 5[ et sur ]5 ; +∞[. Vidéo : étudier algébriquement la continuité d'une fonction 3.

Continuité des fonctions usuelles. Propriétés : • Les fonctions polynômes sont continues sur ℝ. 1 • La fonction inverse 𝑥 ↦ 𝑥 est continue sur ] − ∞ ; 0[ et sur ]0 ; +∞[. • La fonction exponentielle 𝑥 ↦ 𝑒 𝑥 est continue sur ℝ. • • • La fonction racine carrée 𝑥 ↦ √𝑥 est continue sur [0 ; +∞[. Les fonctions 𝑥 ↦ sin 𝑥 et 𝑥 ↦ cos 𝑥.... »