la dérivation

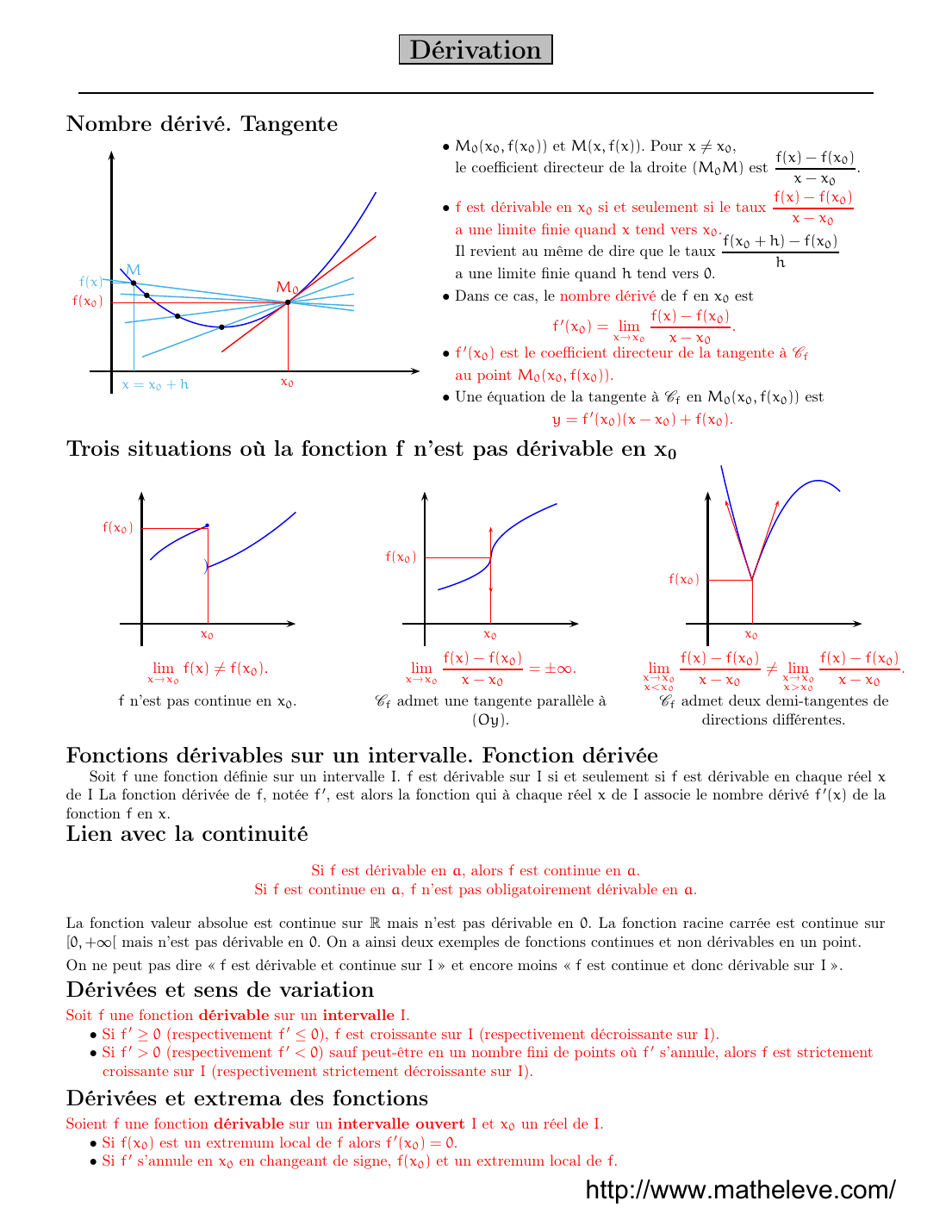
« Dérivation Nombredérivé.Tangente b b b b b M 0 M x0 f(x0) x=x0+h f(x) •M 0(x0,f(x0)) et M (x,f (x)).Pour x6= x0, lecoecientdirecteurdeladroite (M 0M )est f(x) f(x0) xx0 . •festdérivableen x0sietseulementsiletaux f(x) f(x0) xx0 aunelimiteniequand xtendvers x0. Ilrevientaumêmededirequeletaux f(x0+h) f(x0) h aunelimiteniequand htendvers 0. •Danscecas,lenombredérivéde fen x0est f′(x0)= limxx0 f(x) f(x0) xx0 . •f′(x0)estlecoecientdirecteurdelatangenteà Cf aupoint M 0(x0,f(x0)). •Uneéquationdelatangenteà Cfen M 0(x0,f(x0)) est y= f′(x0)(xx0)+ f(x0). Troissituationsoùlafonctionfn’estpasdérivableenx 0 )  f(x0) x0 f(x0) x0 f(x0) x0 limxx0f(x)6= f(x0). limxx0 f(x) f(x0) xx0 = ±. limxx0 xx 0 f(x) f(x0) xx0 . fn’estpascontinueen x0. Cfadmetunetangenteparallèleà (Oy ). Cfadmetdeuxdemi-tangentesde directionsdiérentes. Fonctionsdérivablessurunintervalle.Fonctiondérivée Soit funefonctiondéniesurunintervalle I.festdérivablesur Isietseulementsi festdérivableenchaqueréel x de ILafonctiondérivéede f,notée f′,estalorslafonctionquiàchaqueréel xde Iassocielenombredérivé f′(x)dela fonction fen x. Lienaveclacontinuité Si festdérivableen a,alors festcontinueen a. Si festcontinueen a,fn’estpasobligatoirementdérivableen a. Lafonctionvaleurabsolueestcontinuesur R maisn’estpasdérivableen 0.Lafonctionracinecarréeestcontinuesur [0,+[maisn’estpasdérivableen 0.Onaainsideuxexemplesdefonctionscontinuesetnondérivablesenunpoint. Onnepeutpasdire« festdérivableetcontinuesur I»etencoremoins« festcontinueetdoncdérivablesur I». Dérivéesetsensdevariation Soit funefonction dérivable surun intervalle I. •Si f′≥ 0(respectivement f′≤ 0),festcroissantesur I(respectivementdécroissantesur I). •Si f′>0 (respectivement f′. »