Grand oral surbooking avion

« Comment fonctionne la stratégie de Surbooking des compagnies aériennes? Vous ne le saviez peut-être pas mais ce n'est pas parce que vous avez payé votre billet que vous aurez forcément une place.

En effet, les compagnies aériennes emploient une méthode de “surbooking” en vendant plus de billets qu’il n’y a de places dans l’avion en pariant sur le fait que certains voyageurs manqueraient l’avion.

Cette méthode est tout à fait légale et permet aux compagnies de remplir le plus possible leurs avions.

Cependant elles ne peuvent en vendre un trop grand nombre car elles disposent d’une “pénalité” à chaque fois qu'elles refusent un client. Mais alors comment les mathématiques nous permettent-elles de comprendre cette stratégie du surbooking ? Nous verrons donc comment les compagnies font pour savoir le nombre de places qu’il faut vendre en plus pour être le plus rentable possible sans pour autant tacher leur réputation.

Dans un premier temps je vais utiliser la loi binomiale pour modéliser la situation. Puis je calculerai le gain espéré par une compagnie pour un vol choisi. 1/Schéma de Bernoulli et loi binomiale D'après des estimations plus de 95% des passagers se présentent en moyenne à l'aéroport, seulement nous n’avons pas de chiffres concrets récents des compagnies donc je recrée le schéma. Je suppose qu'environ 97% des voyageurs se présentent à l'embarquement d’un vol Londres-Paris, avec un avion de capacité de 200 places.

D’après mes recherches, le prix de ce vol avec Air France est d’environ 100 euros.

La compagnie choisit de vendre 5 billets en plus soit 205 billets pour 200 places.

De plus, pour un vol de moins de 1500km qui est le cas ici, le remboursement en cas de refus est estimé à 250 euros Soit l’expérience “un passager est absent” contient deux issues : p :” passager présent” de 0.97 1-p :” passager absent” 0.03 La présence d’un passager n’influe pas celle des autres.

On répète donc 205 fois de manière identique et indépendante.

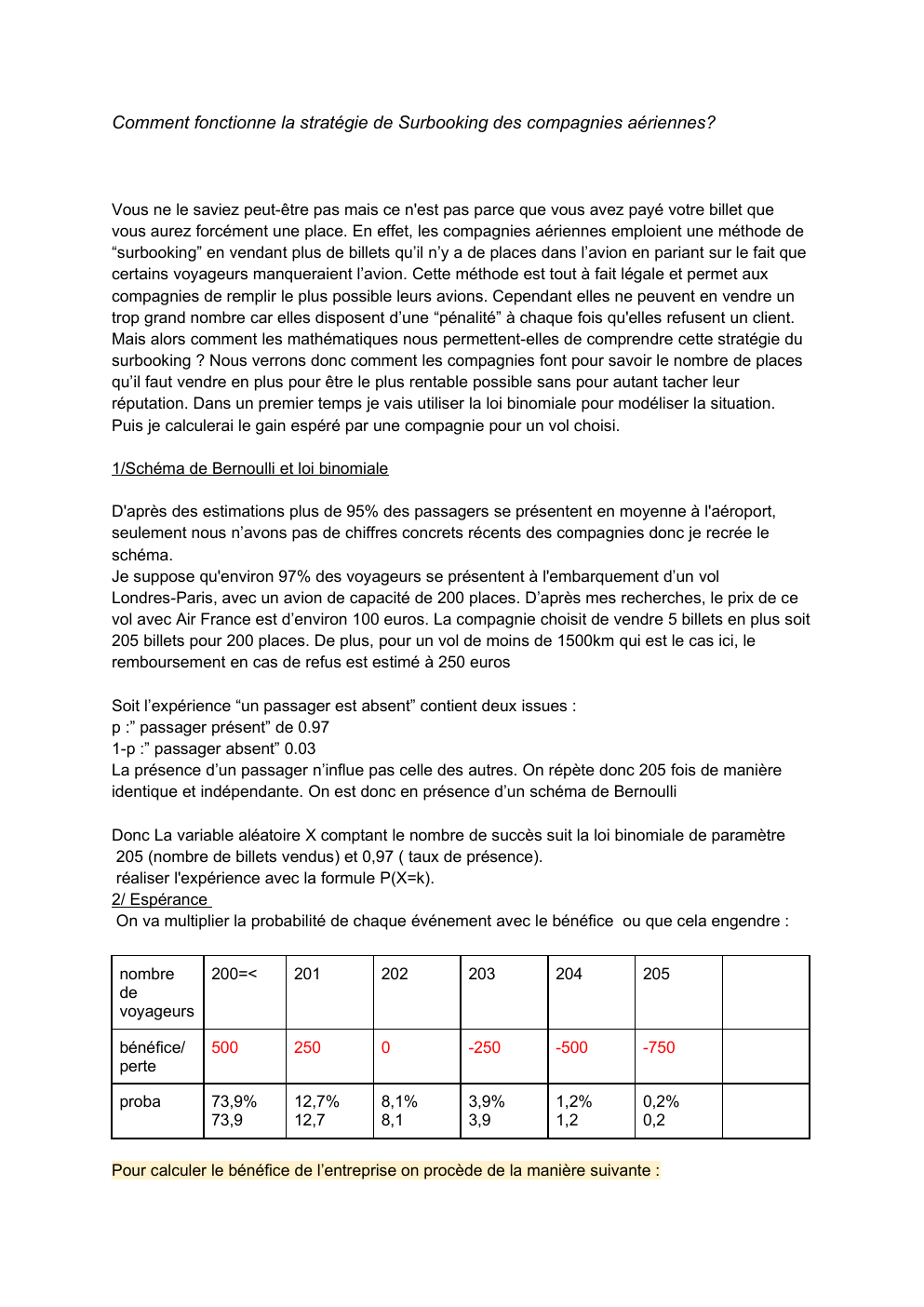
On est donc en présence d’un schéma de Bernoulli Donc La variable aléatoire X comptant le nombre de succès suit la loi binomiale de paramètre 205 (nombre de billets vendus) et 0,97 ( taux de présence). réaliser l'expérience avec la formule P(X=k). 2/ Espérance On va multiplier la probabilité de chaque événement avec le bénéfice ou que cela engendre : nombre de voyageurs 200=< 201 202 203 204 205 bénéfice/ perte 500 250 0 -250 -500 -750 proba 73,9% 73,9 12,7% 12,7 8,1% 8,1 3,9% 3,9 1,2% 1,2 0,2% 0,2 Pour calculer le.... »