Fonction exponentielle

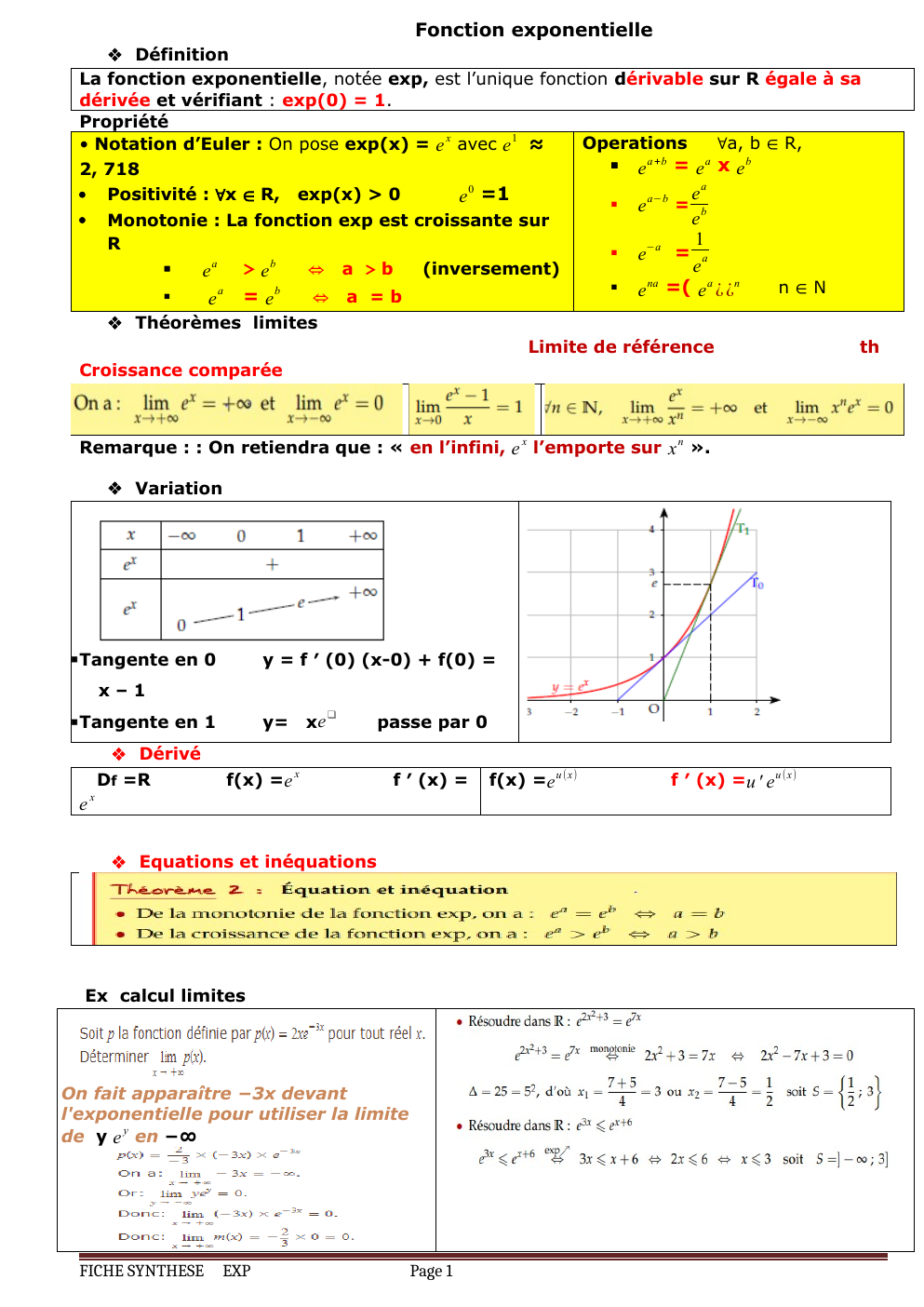
« Fonction exponentielle  Définition La fonction exponentielle, notée exp, est l’unique fonction dérivable sur R égale à sa dérivée et vérifiant : exp(0) = 1. Propriété Operations ∀a, b ∈ R, • Notation d’Euler : On pose exp(x) = e x avec e 1 ≈ a +b a b  = e e xe 2, 718 0 ea  Positivité : ∀x ∈ R, exp(x) > 0 e =1  e a−b = b e  Monotonie : La fonction exp est croissante sur 1 R −a  = e a a e  > eb ⇔ a >b (inversement) e  e na =( e a ¿ ¿n n∈N a b  ⇔ a =b e =e  Théorèmes limites Limite.... »