Fiche Méthodologique : La dérivation

« Fiche Méthodologique : La dérivation Rappelons que cette fiche n’a pas pour principe de présenter la dérivation sous un angle Mathématiques mais sous un aspect pratique. I. La pente d’une droite A. Le concept de « pente » d’une droite Avant de présenter le concept de la dérivation, il est nécessaire de savoir et de maîtriser ce qu’est la pente d’une droite. La pente d’une droite compare l’évolution de « x » et de « f(x) ».

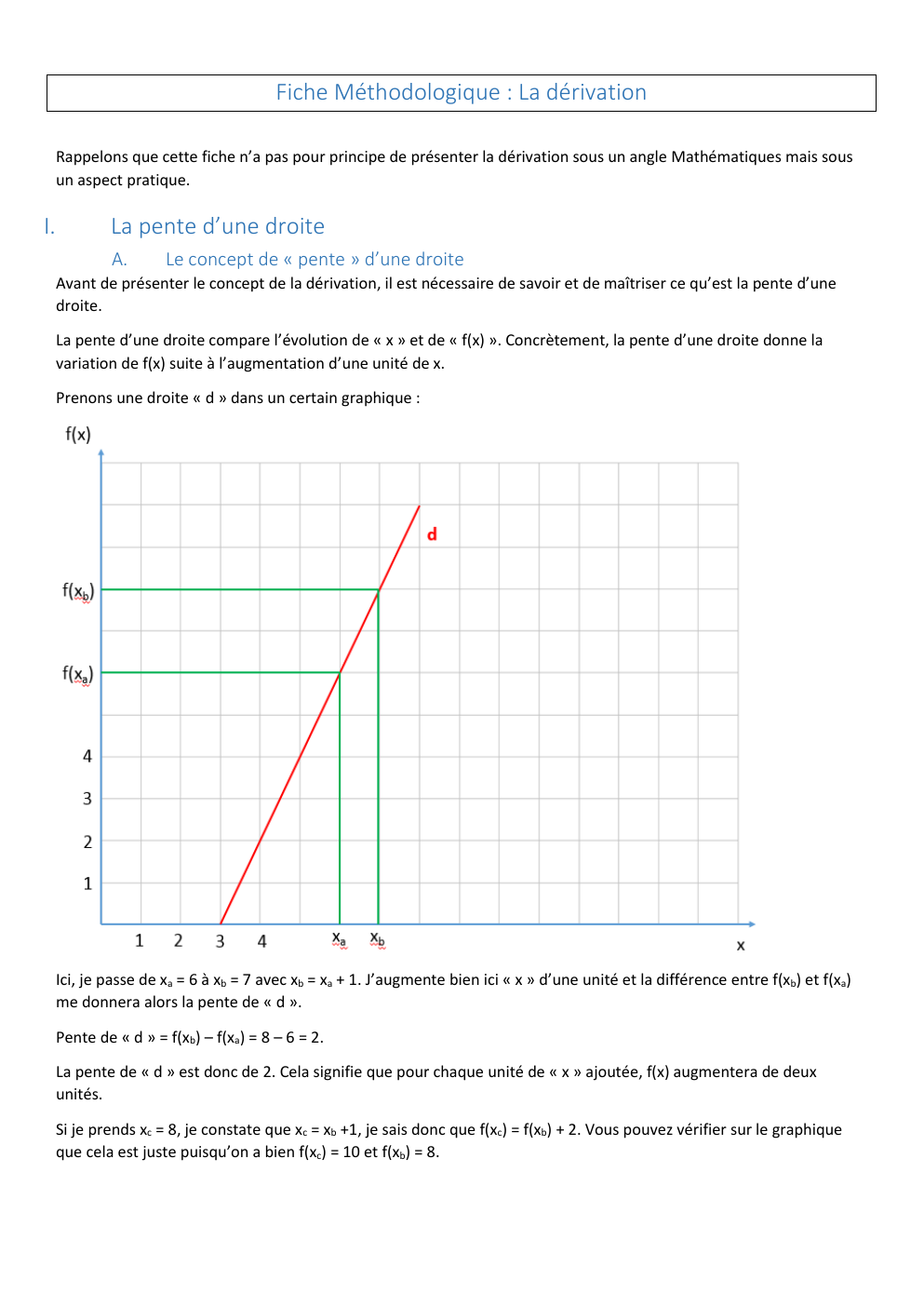
Concrètement, la pente d’une droite donne la variation de f(x) suite à l’augmentation d’une unité de x. Prenons une droite « d » dans un certain graphique : Ici, je passe de xa = 6 à xb = 7 avec xb = xa + 1.

J’augmente bien ici « x » d’une unité et la différence entre f(xb) et f(xa) me donnera alors la pente de « d ». Pente de « d » = f(xb) – f(xa) = 8 – 6 = 2. La pente de « d » est donc de 2.

Cela signifie que pour chaque unité de « x » ajoutée, f(x) augmentera de deux unités. Si je prends xc = 8, je constate que xc = xb +1, je sais donc que f(xc) = f(xb) + 2.

Vous pouvez vérifier sur le graphique que cela est juste puisqu’on a bien f(xc) = 10 et f(xb) = 8. B. La généralisation du concept de pente S’il est vrai que la pente d’une droite nous indique l’augmentation en unités de f(x) suite à l’augmentation d’une unité de x, on peut calculer cette pente grâce à deux points quelconques de cette droite. Regardons avec attention le calcul suivant : En effet, rappelons que : II. De la pente d’une droite au coefficient directeur de la tangente A. Le calcul de la dérivée Si on fait le parallèle entre le calcul de la pente d’une droite et le calcul de la dérivée à une fonction, la ressemblance est immédiate. Rappel, calcul de la dérivée à la fonction f au point x : Ce calcul est donc un calcul de pente entre deux points séparés par une distance qui tend vers 0.

En effet, on aurait pu écrire la formule de la pente d’une droite de la façon suivante : La seule différence entre un calcul de dérivée et un calcul de pente réside donc dans la distance qui sépare les deux points choisis.

Pour la pente, cette distance importe peu tandis que pour la dérivée, cette distance doit tendre vers 0. B. Le concept de tangente Puisque la distance entre les deux points considérés pour cette tangente tend vers 0, on peut considérer qu’à « la limite », les deux points se confondent. Prenons deux points d’une même courbe qu’on va « rapprocher » « à l’infini ».

Ici, si on zoome au fur et à mesure sur ma courbe, je peux bel et bien diminuer ma distance h et construire deux points de plus en plus rapprochés. / !\ On va tracer en vert la droite qui passe par ces deux points afin de vous introduire la notion de « tangente ».

/ !\ Je zoom une première fois sur ma courbe et je peux alors diminuer ma distance « h ». / !\ Le « zoom » n’est pas nécessaire mais il aide.... »