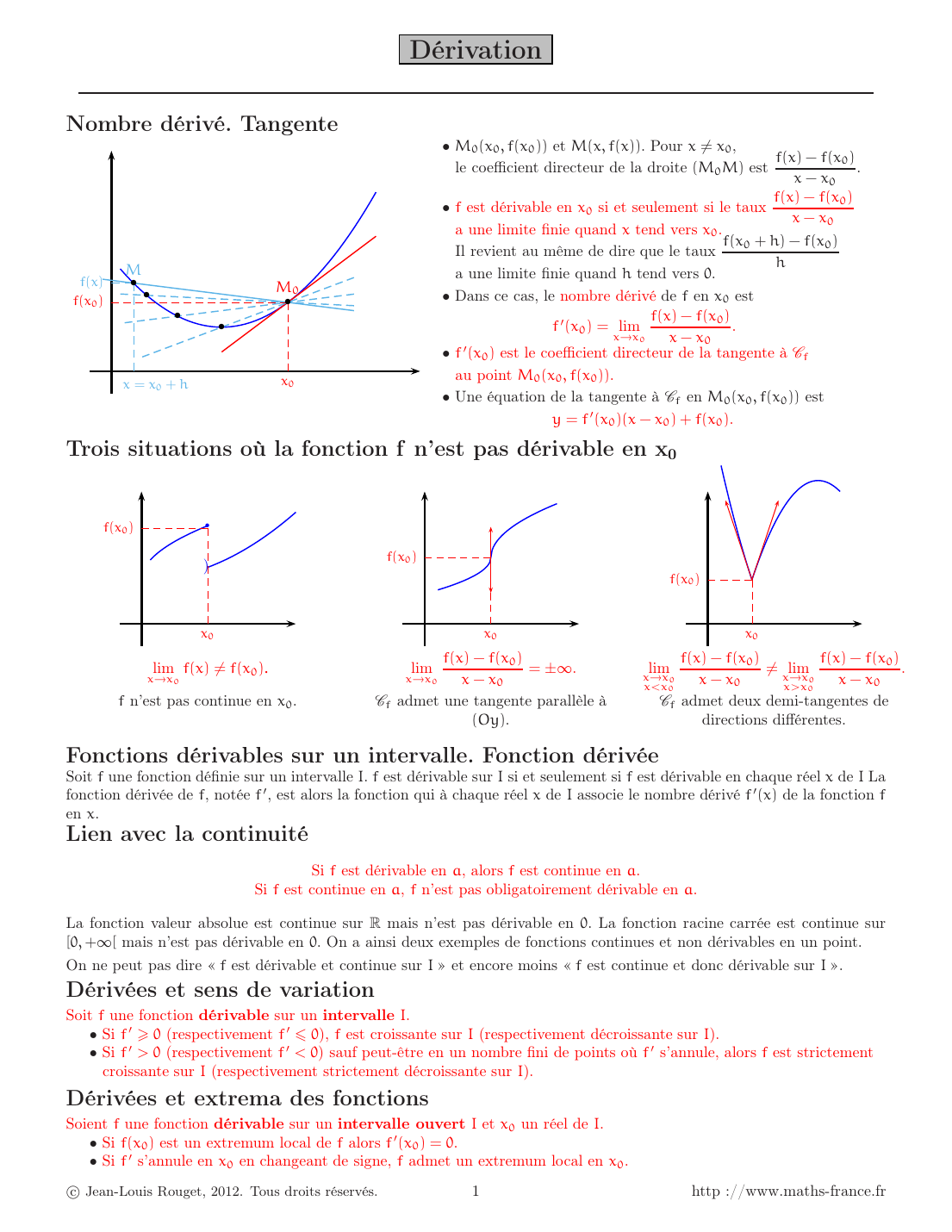
Dérivation

« Dérivation Nombre dérivé.

Tangente b b b b bM 0 M x0 f (x 0) x = x 0 + h f (x ) • M 0( x 0, f (x 0)) et M(x, f (x )) .

Pour x6 = x 0, le coecient directeur de la droite (M 0M )est f (x ) f(x 0) x x 0 . • f est dérivable en x 0 si et seulement si le taux f (x ) f(x 0) x x 0 a une limite nie quand xtend vers x 0. Il revient au même de dire que le taux f (x 0 + h) f(x 0) h a une limite nie quand htend vers 0. • Dans ce cas, le nombre dérivé de fen x 0 est f′ ( x 0) = lim x x 0 f (x ) f(x 0) x x 0 . •f ′ ( x 0) est le coecient directeur de la tangente à C f au point M 0( x 0, f (x 0)) . • Une équation de la tangente à C f en M 0( x 0, f (x 0)) est y= f′ ( x 0)( x x 0) + f(x 0) . Trois situations où la fonction f n’est pas dérivable en x 0 ) f (x 0) x0 f(x 0) x0 f(x 0) x0 lim x x 0 f (x ) 6 = f(x 0) .

lim x x 0 f (x ) f(x 0) x x 0 = ± .

lim x x 0 xx 0f (x ) f(x 0) x x 0 . f n’est pas continue en x 0. C f admet une tangente parallèle à (Oy ).

C f admet deux demi-tangentes de directions diérentes. Fonctions dérivables sur un intervalle.

Fonction dérivée Soit fune fonction dénie sur un intervalle I.

f est dérivable sur Isi et seulement si fest dérivable en chaque réel xde ILa fonction dérivée de f, notée f′ , est alors la fonction qui à chaque réel xde Iassocie le nombre dérivé f′ ( x ) de la fonction f en x. Lien avec la continuité Si fest dérivable en a, alors fest continue en a. Si fest continue en a,f n’est pas obligatoirement dérivable en a. La fonction valeur absolue est continue sur Rmais n’est pas dérivable en 0.

La fonction racine carrée est continue sur [ 0, + [mais n’est pas dérivable en 0.

On a ainsi deux exemples de fonctions continues et non dériv ables en un point. On ne peut pas dire « fest dérivable et continue sur I» et encore moins « fest continue et donc dérivable sur I». Dérivées et sens de variation Soit fune fonction dérivablesur unintervalle I. •Si f′ 0(respectivement f′ 0), fest croissante sur I(respectivement décroissante sur I). •Si f′ > 0 (respectivement f′ < 0 ) sauf peut-être en un nombre ni de points où f′ s’annule, alors fest strictement croissante sur I(respectivement strictement décroissante sur I). Dérivées et extrema des fonctions Soient fune fonction dérivablesur unintervalle ouvert Iet x 0 un réel de I. •Si f(x 0) est un extremum local de falors f′ ( x 0) = 0. •Si f′ s’annule en x 0 en changeant de signe, fadmet un extremum local en x 0. c Jean-Louis Rouget, 2012.

Tous droits réservés.

1 http ://www.maths-france.fr. »