cours sur les intégrales

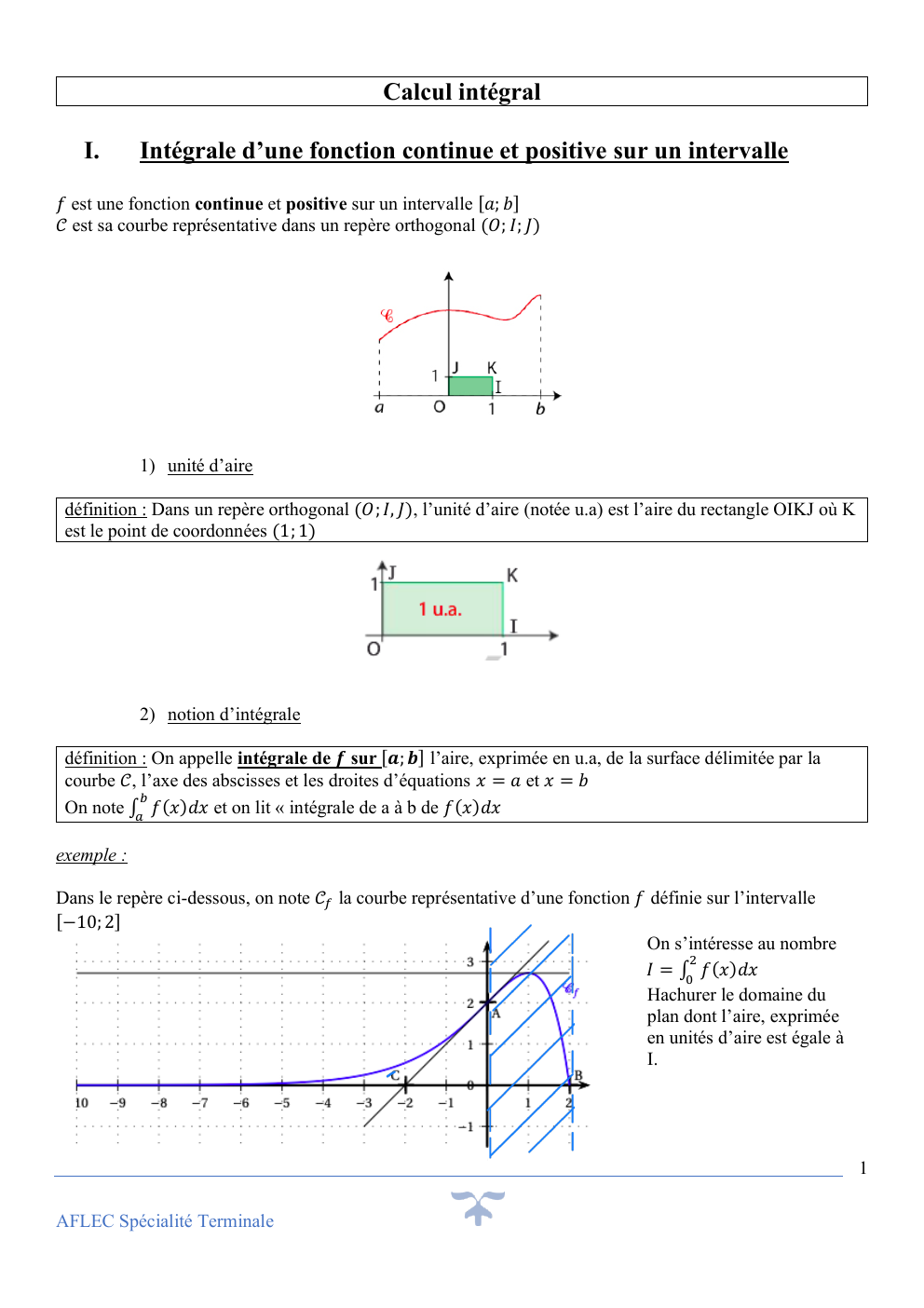
« Calcul intégral I. Intégrale d’une fonction continue et positive sur un intervalle 𝑓 est une fonction continue et positive sur un intervalle [𝑎; 𝑏] 𝒞 est sa courbe représentative dans un repère orthogonal (𝑂; 𝐼; 𝐽) 1) unité d’aire définition : Dans un repère orthogonal (𝑂; 𝐼, 𝐽), l’unité d’aire (notée u.a) est l’aire du rectangle OIKJ où K est le point de coordonnées (1; 1) 2) notion d’intégrale définition : On appelle intégrale de 𝒇 sur [𝒂; 𝒃] l’aire, exprimée en u.a, de la surface délimitée par la courbe 𝒞, l’axe des abscisses et les droites d’équations 𝑥 = 𝑎 et 𝑥 = 𝑏 𝑏 On note ∫𝑎 𝑓(𝑥)𝑑𝑥 et on lit « intégrale de a à b de 𝑓(𝑥)𝑑𝑥 exemple : Dans le repère ci-dessous, on note 𝒞𝑓 la courbe représentative d’une fonction 𝑓 définie sur l’intervalle [−10; 2] On s’intéresse au nombre 2 𝐼 = ∫0 𝑓(𝑥)𝑑𝑥 Hachurer le domaine du plan dont l’aire, exprimée en unités d’aire est égale à I. 1 AFLEC Spécialité Terminale Remarques : 𝑏 • Pour toute fonction continue et positive, ∫𝑎 𝑓(𝑥)𝑑𝑥 est un nombre positif • 𝑥 est une variable « muette » : elle n’intervient pas dans le résultat. 𝑏 𝑏 𝑏 On peut noter indifféremment ∫𝑎 𝑓(𝑥)𝑑𝑥 = ∫𝑎 𝑓(𝑡)𝑑𝑡 = ∫𝑎 𝑓(𝑢)𝑑𝑢 = ⋯ 3) quelques exemples 2 exemple 1 : Calculer ∫0 0,75𝑥𝑑𝑥 2 AFLEC Spécialité Terminale 3 exemple 2 : Calculer ∫1 (−2𝑡 + 8)𝑑𝑡 exemple 3 : 𝑔 est la fonction définie sur [−3; 4] par : −𝑥 + 2 si − 3 ≤ 𝑥 ≤ 1 𝑔(𝑥) = { 3𝑥 − 2 si 1 < 𝑥 ≤ 4 a) Tracer la courbe représentative de la fonction 𝑔 dans un repère orthonormé b) La fonction 𝑔 est-elle positive, continue sur l’intervalle [−3; 4]? Justifier graphiquement. 4 c) Déterminer ∫−3 𝑔(𝑥)𝑑𝑥 3 AFLEC Spécialité Terminale II. Intégrale et primitive 1) théorème fondamental théorème : 𝑓 est une fonction continue et positive sur un intervalle [𝑎 ; 𝑏]. 𝑥 La fonction 𝐹𝑎 : 𝑥 ⟼ ∫𝑎 𝑓(𝑡)𝑑𝑡 est la primitive de la fonction 𝑓 sur l’intervalle [𝑎 ; 𝑏] telle que 𝐹𝑎 (𝑎) = 0 démonstration : On démontre le cas où 𝑓 est strictement croissante sur [𝑎; 𝑏]. 2) calcul d’une intégrale à l’aide d’une primitive 𝑏 propriété : Pour toute primitive 𝐹 de 𝑓 sur l’intervalle [𝑎; 𝑏], ∫𝑎 𝑓(𝑥)𝑑𝑥 = [𝐹(𝑥)]𝑏𝑎 = 𝐹(𝑏) − 𝐹(𝑎) exemple 1: 𝑓 est la fonction définie sur l’intervalle 𝐼 = [0; +∞[ par : 𝑥 2 + 6𝑥 𝑓 (𝑥 ) = (𝑥 + 3)2 𝑥2 a) Vérifier que la fonction F définie par 𝐹(𝑥) = 𝑥+3 est une primitive de 𝑓 sur I. 3 b) Calculer ∫1 𝑓(𝑥)𝑑𝑥 exemple 2 : Dans chaque cas, déterminer l’intégrale à l’aide d’une primitive. 2 a) ∫1 𝑥 3 𝑑𝑥 1 b) ∫−1 𝑒 −𝑥 𝑑𝑥 4 AFLEC Spécialité Terminale III.

Intégrale d’une fonction continue de signe quelconque sur un intervalle. 1) extension de la définition de l’intégrale théorème : Toute fonction continue sur un intervalle I admet des primitives sur I. définition : 𝑓 est une fonction continue de signe quelconque sur un.... »