Algèbre linéaire et géométrie vectorielle Préparatoire de l’examen
Publié le 28/04/2022
Extrait du document
«
Algèbre linéaire et géométrie vectorielle
Préparatoire de l’examen 3
No 1
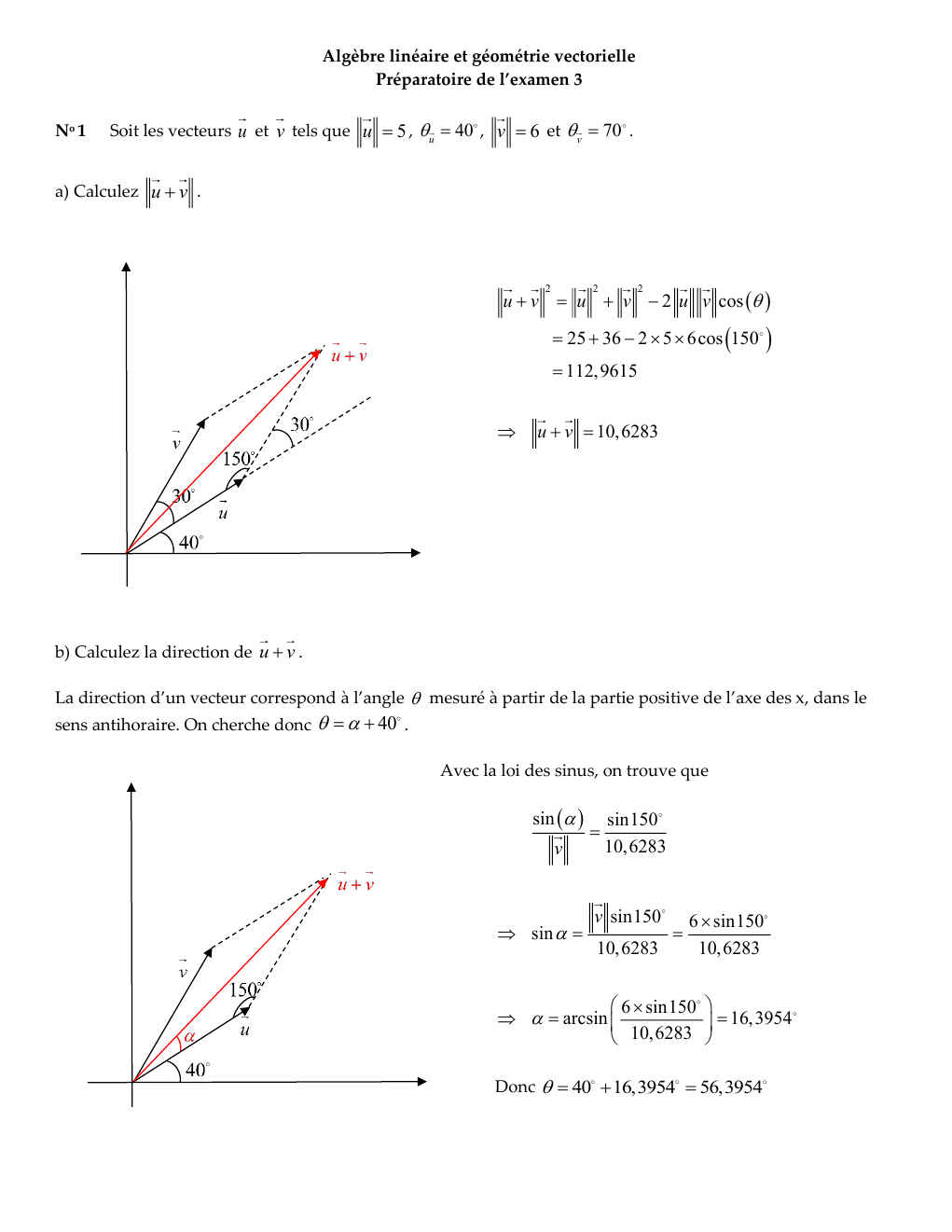
Soit les vecteurs u et v tels que u = 5 , u = 40 , v = 6 et v = 70 .
a) Calculez u + v .
u + v = u + v − 2 u v cos ( )
2
2
2
= 25 + 36 − 2 5 6cos (150
)
= 112,9615
u + v = 10,6283
b) Calculez la direction de u + v .
La direction d’un vecteur correspond à l’angle mesuré à partir de la partie positive de l’axe des x, dans le
sens antihoraire.
On cherche donc = + 40 .
Avec la loi des sinus, on trouve que
sin ( )
v
sin =
=
sin150
10,6283
v sin150
10,6283
=
6 sin150
10,6283
6 sin150
= arcsin
= 16,3954
10,6283
Donc = 40 + 16,3954 = 56,3954.
»
↓↓↓ APERÇU DU DOCUMENT ↓↓↓
Liens utiles
- Évariste Galois1811-1832Galois étudia à Louis-le-Grand où il rencontra Louis Richard, qui encouragea cet élèvebrillant à lire des ouvrages d'algèbre et la géométrie de Lagrange et de Laplace.
- VIETE, François (1540-1603)Mathématicien, il crée l'algèbre, ouvre la voie à la géométrie analytique en appliquant l'algèbre à la géométrie.
- Objet d'étude : La poésie du XIX et du XX siècle. Parcours complémentaire : Alchimie poétique : réinventer le monde. Analyse linéaire 2/2 « Le Pain », Francis Ponge, Le Parti pris des choses, 1942
- Étude linéaire n°2 – Les Fausses Confidences, Marivaux, 1737 – Acte II, scène 13 : le stratagème d’Araminte
- Lecture linéaire - L'Huitre de Francis Ponge